Perlin noise
Perlin noise에 대하여 간단한 정리
Perlin Noise

일반적으로 이야기하는 노이즈(white noise)는 인접한 값들이 서로 어떠한 관계도 갖지 않는다.
즉, 각 모두 무작위 값으로 나열되어 있다.
이런 형태의 노이즈는 인접한 값 사이의 변화가 매우 급격하다.
그래서 무작위적 요소가 작용하는 곳에는 사용할 수 있지만, 점진적 변화가 필요한 곳에는 사용하기가 부적합하다.

Perlin noise는 떨어진 두 무작위 값(gradient) 사이를 보간된 값들로 채워넣는 방식으로 생성된다.
따라서 White noise와 달리 인접한 값 사이의 변화가 적고, 부드러운 값의 변화를 갖는다.
How to make Perlin noise
Perlin noise를 만드는 과정은 차원(1D, 2D, 3D …)에 따라 크게 달라지지 않는다.
핵심은 무작위 값을 갖는 gradient들을 정의하고 그 사이의 값을 보간을 통해 채워나가는 것이다.
1D Perlin noise
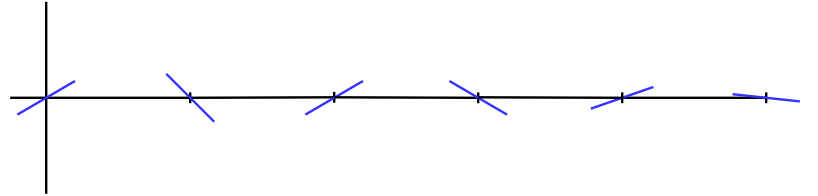
1차원 Perlin noise는 하나의 입력(x)에 대하여 하나의 Noise value(y)를 출력한다.
먼저 각 $x= 0, 1, 2, …i, (i = integer)$마다 [-1.0, 1.0]범위의 gradient를 정한다.
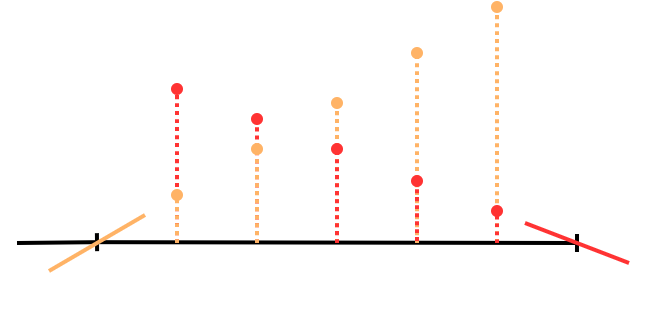
이제 인접한 두 gradient 사이를 보간해야 한다.
기울기가 $m$인 직선의 방정식은 $y = m(x - x_0)$로 나타낼 수 있다.
두 gradient를 각각 $a$와 $b$라 하면 각각의 직선 방정식은
$$
u = a(x - x_a) \\
v = b(x - x_b)
$$
으로 나타낼 수 있다.
$x_a$와 $x_b$ 사이의 점 $x_0$에서 Perlin noise값 $p$는 해당 점에서의 $u, v$값을 선형 보간(Linear interpolation, lerp) 하여 얻는다.
$$
lerp(t, a, b) = bt + a(1 - t) \\
p = lerp(x_0 - x_a, u, v)
$$
우리는 $u$와 $v$를 $t( = x_0 - x_a)$에 대해 보간한다. 여기서 중요한 점은 $u, v$도 모두 $t$에 관한 함수라는 것이다.
$x = t$일때, $u = at$, $v = b(t - 1)$의 값을 갖는다. 이 둘을 $t$에 대하여 보간을 하면
$$
\begin{split}
p &= vt + u(1 - t) \cr
&= b(t - 1)t + at(1 - t) \cr
&= (a - b)(t - t^2)
\end{split}
$$
$t = 0$과 $t = 1$을 x절편으로 하는 포물선 방정식을 얻을 수 있다.
유도된 식에 따르면 $p$는 $t = 0.5$일때 $\frac{a - b}{4}$라는 최대 혹은 최소값을 갖는다. 우리는 Perlin noise에서 [-1, 1]의 범위를 갖는 gradient를 사용하므로 $a - b$의 범위는 [-2, 2]이고, 결국 $p$는 [-0.5, 0.5]의 범위를 갖는다.
이것이 선형 보간을 거치면 그 범위가 처음의 절반이 되는 이유이다.
선형 보간은 말그대로 값을 선형적으로 보간한다. 위 식에서 $t$가 0 혹은 1에 가까워진다해도 여전히 반대편이 값에 영향을 끼친다.
이처럼 $t$가 양 끝에 있을때, 반대편의 영향력을 줄이기 위해서 선형 보간전에 $t$에 대해서 SmoothStep을 적용한다.
$$
SmoothStep(x) = \cases{
0 & x $\le$ 0 \cr
3x2-2x3 & 0 $\le$ x $\le$ 1 \cr
1 & 1 $\le$ x
}
$$
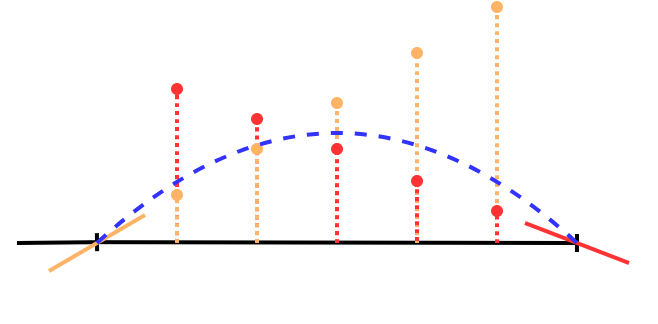
이 단계를 거치게 되면 두 gradient사이를 부드러운 곡선으로 채울 수 있다.
2D Perlin noise

2D역시 1D와 크게 다르지않다. 1D에서는 x축의 정수점마다 [-1, 1]범위의 무작위gradient를 생성하였다.
2D에서는 2차원 grid를 만들고 그리드의 각 교차점마다 길이가 1인 무작위 2차원 unit vector를 생성하여 gradient로 사용한다.
그리드 내부의 점 $p$의 Perlin noise값은 해당 그리드가 가지고있는 4개의 gradient와 각각의 그리드 교차점에서 내부의 점 $p$로의 벡터를 내적한 값(influence)을 보간하여 얻는다.
influence는 하나의 gradient vector($\vec{g}$)와 다른 벡터($\vec{p}$)의 내적이다.
먼저 두 벡터의 내적은 다음과 같이 나타낼 수 있다.
$$
\vec{g}\cdot\vec{p} = |g||p|\cos{\theta}
$$
gradient vector인 $\vec{g}$는 길이가 1인 unit vector이므로
$$
\vec{g}\cdot\vec{p} = |p|\cos{\theta}
$$
$\cos{\theta}$는 두 벡터 사이의 각에 따라서 [-1, 1]의 범위를 갖는다.
$|p|$는 그리드의 꼭지점에서 그리드 내부의 점 $p$로의 벡터의 길이이다.
해당 벡터를 $p’(=\vec{p}-\vec{g})$라 하면
$$|p| = \sqrt{p’_x p’_x + p’_y p’_y}$$
그리드는 한 변의 길이가 1인 정사각형이므로 $|p|$는 [-$\sqrt{2}$, $\sqrt{2}$]의 범위를 갖는다.
내적을 통해 얻은 4개의 값 $u,v,s,t$를 내부의 점$p$의 상대좌표 $(x’, y’) = p - p_0$를 x축 방향, y축방향으로 보간한다.
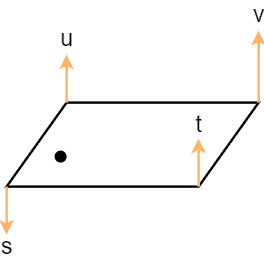
$$
ix0 = lerp(x’, u, v) \\
ix1 = lerp(x’, s, t) \\
p = lerp(y’, ix0, ix1)
$$
보간을 거치면서 크기가 반으로 줄어든다는 점을 잊지말자.
1D때와 마찬가지로 $(x’, y’)$를 보간하기 전에 $SmoothStep$을 적용한다.
위에서 살펴본것처럼 1D의 과정과 크게 다르지 않다.
다른점이 있다면 입력으로 1개(x)가 아닌 2개(x, y)의 값이 사용된다는 점과 보간하는 축이 늘어남에따라 보간의 수가 늘었다는 것 정도이다.(보간에 의한 크기 감소는 보간의 횟수와는 관계가 없다.)
그리고 Perlin noise값의 범위가 [-0.5, 0.5]에서 [-0.5 * $\sqrt{2}$, 0.5 * $\sqrt{2}$]로 바뀌었다는 것이다.
3D Perlin noise and more
2D 과정 마지막에 말한 것 처럼 차원이 증가한다고 해서 그 과정이 크게 변한다거나 하지 않는다.
다음 차원은 충분히 머리속으로 생각해볼 수 있을 것이다.
3D 에서는 축이 3개이므로 그리드로 3차원 cube를 사용 할 것이고, gradient는 3차원 unit vector를 사용 할 것이다.
최종 노이즈 값은 8개의 influence를 x축, y축, z축에 대하여 보간한 값이고, 그 범위는 [-0.5 * $\sqrt{3}$, 0.5 * $\sqrt{3}$]이 될 것이다.
3차원을 넘어서 n-차원에서도 이는 동일하게 적용된다.
Octave
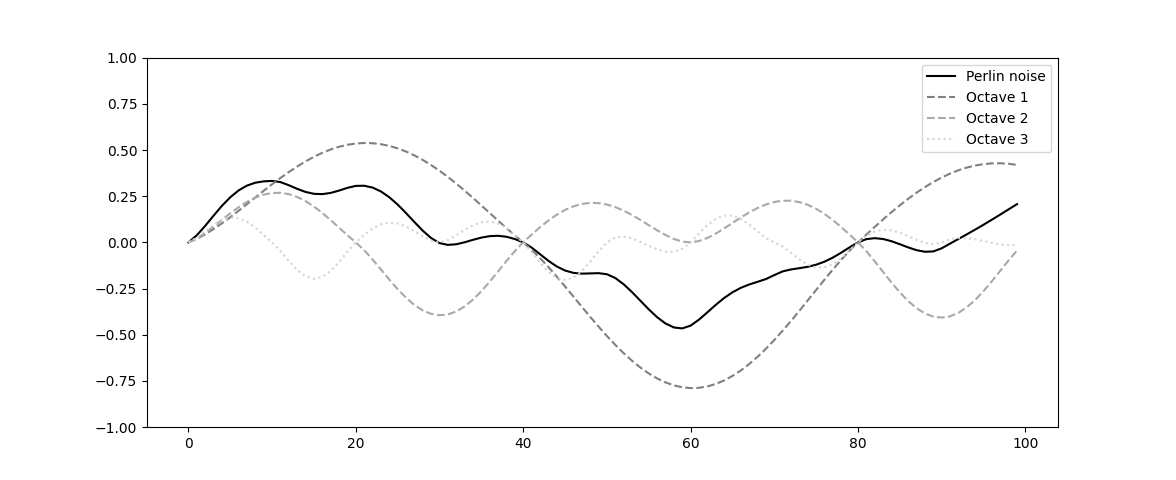
$2^n, (n = 0, 1, 2, …)$의 resolution을 갖고(보간하는 $t$의 간격이 $2^{-n}$) 크기도 $2^{-n}$배인 Perlin noise를 추가로 생성하고 합친다.
합쳐지는 각각의 Perlin noise를 Octave라 부른다.(음악에서 1옥타브는 원음의 두배의 주파수를 갖는다.)
Octave = k인 Perlin noise는 $\pm \frac{\sqrt{k}}{2^{k}}$의 범위를 갖는다.